二叉树

发表于   |   更新于 | 分类于
字数统计: 4.2k

二叉树学习笔记

基本概念

二叉树可以定义为节点的有限集合，这个集合或者为空集，或者由一个根及两棵不相交的分别称作这个根的左子树和右子树的二叉树组成。（二叉树的定义是一个递归定义），二叉树可以是空集合，此时的二叉树称为空二叉树；二叉树也可可以是只有一个节点的集合，这个节点只能是根；它的左子树和右子树均是空二叉树。（图片源自张乃孝$PPT$）

  • 满二叉树：如果一棵二叉树的任何节点或者是树叶，或有两棵非空子树，则此二叉树称作满二叉树。
  • 完全二叉树：如果一棵二叉树至多只有最下面的两层节点读书可以小于2，其余各层节点度数^节点分支数^都必须为2，并且最下面一层的节点都集中在该层最左边的若干位置上，则此二叉树称为完全二叉树。（完全二叉树不一定是满二叉树）
  • 扩容二叉树：把原二叉树的节点都变为度数为2的分支节点，也就是说，如果原节点的度数为2，则不变；度数为1，则增加一个分支；度数为0，则增加两个分支。新增加的节点都用小方框表示，称为外部节点，树中原有的节点称为内部节点。特别地，对空二叉树扩容得到的扩容二叉树只有一个外部节点。
  • 外部路径长度E:在扩容的二叉树中从根到每个外部节点的路径长度之和。内部路径长度I：在扩容的二叉树中从根到每个内部节点的路径长度之和。

主要性质

1、在二叉树的$i$层上至多有$2^i$个节点（$i\ge 0$）

2、高度为$k$的二叉树中最多有$2^{k+1}-1$个节点（$k \ge 0$）

3、对于任何一棵二叉树，如果叶节点个数为$n_{0}$，度^1为2的节点个数为$n_{2}$，则有：$n_{0}=n_{2}+1$。（$n_{0}+n_{1}+n_{2}=n_{1}+2*n_{2}+1$）

4、具有$n$个节点的完全二叉树的深度$k$为$[log_{2}n]$。

5、对于具有$n$个节点的完全二叉树，如果按照从上（根节点）到下（叶节点）和从左到右的顺序对二叉树中的所有节点从0开始到$n-1$进行编号，则对于任意的下表为$i$的节点，有：

​ (1).如果$i=0$，则它是根节点，它没有父节点；如果$i\gt 0$，则它的父节点的下表为$[(i-1)/2]$；

​ (2).如果$2i+1 \le n-1$，则下标为$i$的节点的下标为$2i+1$；否则，下标为$i$的节点没有左子节点；

​ (3).如果$2i+2 \le n-1$，则下标为$i$的节点的右子节点的下标为$2i+2$；否则，下标$i$的节点没有右子节点。

6、在满二叉树中，叶节点的个数比分支节点个数多1。（$n_{0}=n_{2}+1$）

7、在扩充二叉树中，外部节点个数比内部节点个数多1。

8、对任意扩充二叉树，外部路径长度$E$和内部路径长度$I$之间满足关系：$E=I+2n$，其中$n$是内部节点个数。

抽象数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
ADT BinTree is
    operations
    BinTree createEmptyBinTree(void)/*创建一棵空的二叉树*/
    BinTree consBinTree(BinTreeNode root,BinTree left,BinTree right)/*返回一棵二叉树，其根节点是root，左右二叉树分别为left和right。*/
    int isNull(BinTree t)/*判断二叉树t是否为空*/
    BinTreeNode root(BinTree t)/*返回二叉树t的根节点。若为空二叉树，则返回一特殊值*/
    BinTreeNode parent(BinTree t,BinTreeNode p)
    /*返回节点p的父节点，当指定的节点为根时，返回一个特殊值*/
    BinTree leftChild(BinTree t,BinTreeNode p)
    /*返回p节点的左子树，当指定节点没有左子树时，返回一个特殊值*/
    BinTree rightChild(BinTree t,BinTreeNode p)
    /*返回p节点的右子树，当指定节点没有右子树时，返回一个特殊值*/
end ADT BinTree

二叉树的周游

二叉树的周游是指按某种方式访问二叉树中的所有节点，使每个节点被访问一次且只能被访问一次。

深度优先周游

若以符号$D$、$L$、$R$分别表示根节点、左子树、右子树，则二叉树的周游共有六种方式：$DLR$、$LDR$、$LRD$、$DRL$、$RDL$和$RLD$。如果限定先左后右，则只能采用前三种周游方式：

  • $DLR$ <—-> 先根次序（简称先序或前序）周游

若二叉树不空，则先访问根；然后按先根次序周游左子树；最后按先根次序周游右子树。$eg$.下图二叉树先根次序周游得到的节点序列为：A、B、D、C、E、G、F、H、I。

  • $LRD$ <—-> 后根次序（简称后序）周游

若二叉树不空，则先按后根次序周游左子树；然后按后根次序周游右子树；最后访问根。上图所示的二叉树，后根次序周游得到的节点序列为：D、B、G、E、H、I、F、C、A。

  • $LDR$ <—-> 中根次序（简称中序或对称序）周游

若二叉树不空，则先按对称序周游左子树，然后访问根；最后按对称序周游右子树。前图所示的二叉树，按对称序周游一棵二叉树得到的节点序列为：D、B、A、E、G、C、H、F、I。

对于给定的二叉树，可以唯一确定它的先根序列、后根序列和对称序列。但是反过来，给定一个二叉树的任意一种周游的序列，无法唯一确定这个二叉树。如果已知一个二叉树的对称序列，又知道另外一种周游序列就可以唯一确定这个二叉树。

广度优先周游

若二叉树的高度为$h$，则从0到$h$逐层如下处理：从左到右逐个访问存在的节点。广度优先周游一棵二叉树所得到的节点序列，叫做这棵二叉树的层次序列。前图二叉树广度优先周游所得到的节点层次序列为：A、B、C、D、E、F、G、H、I。

$eg$.对下图二叉树进行先根、后根和中根周游所得到的线性序列分别为：

图片 结果

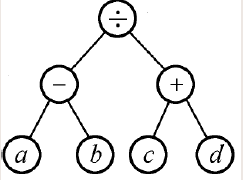上述结果分别被称为表达式的前缀表达式、后缀表达式和中缀表达式。

周游的抽象算法

递归算法
  • 先根次序周游
1
2
3
4
5
6
7
void preOrder(BinTree t){
    if(t==NULL)
        return;
    visit(root(t));
    preOrder(leftChild(t));
    preOrder(rightChild(t));
}
  • 对称序周游
1
2
3
4
5
6
7
void inOrder(BinTree t){
    if(t==NULL)
        return;
    inOrder(leftChild(t));
    visit(root(t));
    inOrder(rightChild(t));
}
  • 后根次序周游
1
2
3
4
5
6
7
void postOrder(BinTree t){
    if(t==NULL)
        return ;
    postOrder(leftChild(t));
    postOrder(rightChild(t));
    visit(root(t));
}
非递归算法
  • 先根次序周游
  1. 把根节点压入栈中；2、从栈顶中取出元素（包括退栈），只要取出元素非空，就访问该节点；3、顺序将其右子节点和左子节点进栈。重复执行2、3，直到当从栈顶中取出的元素（包括退栈）为空，并且栈也为空时，周游结束。

算法时间代价：假设栈的主要操作只要常量时间，算法中每个二叉树恰好进栈、出栈各一次，所以它的时间代价为$O(n)$，其中$n$为二叉树中子二叉树（也是节点）的个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void nPreOrder(BinTree t){
    Stack s;/*栈元素的类型是BinTree*/
    BinTreeNode *c;
    if(t==NULL)
        return ;
    s = createEmptyStack();
    push(s,t);
    while(!isEmptyStack(s){/*每当栈不为空*/
        c = top(s);pop(s);	/*取栈顶，出栈*/
        if(c!=NULL){
            visit(root(c));/*访问*/
            push(s,rightChild(c));/*右子树进栈*/
            push(s,leftChild(c));/*左子树进栈*/
        }
    }
}
  • 对称序周游

1、若当前二叉树不为空时，则沿其左子树尽量前进，在前进过程中，把所经过的二叉树逐个压入栈中，知道左子树为空。

2、弹出栈顶元素为当前二叉树，并访问该二叉树的根；

3、如果当前二叉树有右子树，再进入它的右子树（作为当前二叉树），从1开始执行上述过程；

4、如果当前二叉树没有右子树，但是栈不空，转2。

重复上述过程，直到当前二叉树没有右子树并且栈也为空时，周游结束。

算法时间代价：假设栈的主要操作只要常量时间，算法中每个二叉树恰好进栈、出栈各一次，所以它的时间代价为$O(n)$，其中$n$为二叉树中子二叉树（也是节点）的个数。（外表看上去是一个双重循环，但时间代价还是线性的）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void nInOrder(BinTree t){
    Stack s = createEmptyStack();/*栈元素类型为BinTree*/
    BinTree c = t;
    if(c==NULL)
        return ;
    do{
        while(c!=NULL){
            push(s,c);
            c=leftChild(c);
        }
        c=top(s);pop(s);visit(root(c));
        c=rightChild(c);
    }while(c!=NULL || !isEmptyStack(s));
}
  • 后根次序周游

1、首先由该二叉树找到其左子树，周游其左子树，周游完返回到这个二叉树的根；

2、然后由该二叉树找到其右子树，周游其右子树，周游完再次返回到这个二叉树的根；

3、最后才能访问该二叉树的根结点。

为此必须在算法中增加对二叉树出栈的判断： 如果是从栈顶二叉树的左子树回来，就直接进入右子树周游；如果是从栈顶二叉树的右子树回来，就执行出栈，访问该二叉树的根结点。（时间代价仍为$O(n)$）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void nPostOrder(BinTree t){
    Stack s = createEmptyStack();
    BinTree p = t;
    while(p!=NULL || !isEmptyStack(s)){
        while(p!=NULL){
            push(s,p);
            p=leftChild(p)?leftChild(p):rightChild(p);
            /*循环到当前需要处理的节点*/
		}
        p=top(s);pop(s);visit(root(p));
        /*栈顶二叉树的根时应访问节点*/
        if(!isEmptyStack(s) && leftChild(top(s)==p))
            p=rightChild(top(s));/*栈不空，且为从左子树退回*/
        else p=NULL;/*从右子树回来，推到上一层处理*/
    }
}
  • 广度优先周游

首先把二叉树送入队列；其后，每当从队首取出一个二叉树访问根之后，马上把它的子二叉树按从左到右的次序送入队列尾端；重复此过程直到队列为空。

算法代价：每个二叉树进队列一次出队列一次，所需时间代价为$O(n)$。主要空间代价时需要队列的附加空间。若二叉树节点个数为$n$，最坏的情况出现再完全二叉树时，需要大约$n/2$个队列元素的空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void levelOrder(BinTree t){
    BinTree c,cc;
    Queue q=createEmptyQueue();
    if(t==NULL)
        return ;
    c=t;enQueue(q,c);/*将二叉树送入队列*/
    while(!isEmptyQueue(q)){
        c=frontQueue(q);deQueue(q);visit(root(c));
        /*从队列首部取出二叉树并访问*/
        cc=leftChild(c);if(cc!=NULL) enQueue(q,cc);
        /*将左子树送入队列*/
        cc=rightChild(c);if(cc!=NULL) enQueue(q,cc);
        /*将右子树送入队列*/
    }
}

二叉树的实现

顺序表示

采用一组连续的存储单元来存放二叉树中的节点

对于完全二叉树，按照从上（根节点）到下（叶节点）和从左到右的顺序，对二叉树中的所有节点从0到$n-1$编号，这样存放到一维数组中，只要通过数组元素的下标关系，就可以确定二叉树中节点之间的逻辑关系。

对于一般的二叉树，采用顺序表示，首先要对它进行扩充，增加一些并不存在的空节点，使之成为一棵完全二叉树，然后再用一维数组顺序存储。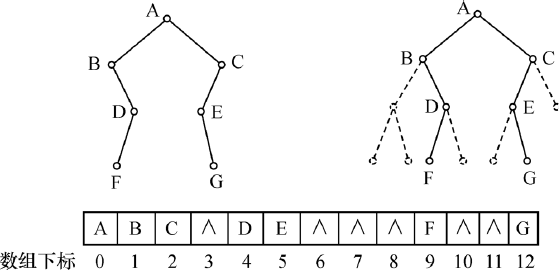

定义
1
2
3
4
5
6
7
struct SeqBinTree{	/*顺序二叉树类型定义*/
    int MAXNUM;	/*完全二叉树中允许节点的最大个数*/
    int n;	/*改造成完全二叉树后，节点的实际个数*/
    DataType * nodelist;	/*存放节点的数组*/
};	
typedef struct SeqBinTree * PSeqBinTree;
/*顺序二叉树类型的指针类型*/
运算实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/*返回下标为p的节点的父节点的下标*/
int parent_seq(PSeqBinTree t,int p){
    if(p<0 || p>= t->n)
        return -1;
    return (p-1)/2;
}

/*返回下标为p的节点的左子节点的下标*/
int leftChild_seq(PSeqBinTree t,int p){
    if(p<0 || p>= t->n) 
        return -1;
    return 2*p+1 /*可能不存在*/
}

/*返回下标为p的节点的右子节点的下标*/
int rightChild_seq(PSeqBinTree t,int p){
    if(p<0 || p>= t->n)
        return -1;
    return 2*(p+1);/*可能不存在*/
}

链接表示

二叉树中的每个节点对应链表中的一个节点，每个节点中，除了存储节点本身的数据外，再设置两个指针字段：llink和rlink，分别存储节点的左子节点和右子节点的位置。当节点的某个子树为空时，则相应的指针为空指针。这种表示方法称为左-右指针表示法。

定义
1
2
3
4
5
6
7
8
struct BinTreeNode;	/*二叉树中节点*/
typedef struct BinTreeNode *PBinTreeNode;
/*节点的指针类型*/
struct BinTreeNode{
    DataType info;	/*数据域*/
    PBinTreeNode llink;	/*指向左子节点*/	
    PBinTreeNode rlink;	/*指向右子节点*/
};
运算实现
1
2
3
4
5
6
7
8
9
10
11
12
13
/*返回节点p的左子节点的地址*/
PBinTreeNode leftChild_link(PBinTreeNode p){
    if(p==NULL)
        return NULL;
    return p->llink;
}

/*返回节点p的右子节点的地址*/
PBinTreeNode rightChild_link(PBinTreeNode p){
    if(p==NULL)
        return NULL;
    return p->rlink;
}
线索二叉树

线索二叉树是对于左-右指针表示法的一种修改，它利用节点的空左指针（$llink$)存储该节点再某种周游序列中的前驱节点的位置；利用节点的空右指针（$rlink$）存储该节点在同种周游序列中的后继节点的位置。这种附加的指向前驱节点和后继节点的指针称作线索，加进了线索的二叉树左-右指针表示称作线索二叉树。

为区分左右指针和线索，需要在每个节点里增加两个标志位$ltag$,和$rtag$。

增加了标志域的节点结构为：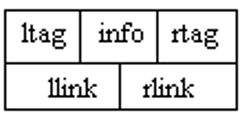

线索二叉树示例：

线索二叉树定义
1
2
3
4
5
6
7
8
9
10
11
struct ThrTreeNode;	/*线索二叉树中的节点*/
typedef struct ThrTreeNode * PThrTreeNode;
/*指向线索二叉树节点的指针类型*/
struct ThrTreeNode{	/*线索二叉树中节点的定义*/
    DataType info;
    PThrTreeNode llink,rlink;
    int ltag,rtag;
};
typedef struct ThrTreeNode * ThrTree;
/*线索二叉树类型的定义*/
typedef ThrTree * PThrTree;/*线索二叉树类型的指针类型*/
按对称序线索化二叉树

在未线索化之前，所有结点的$llink$和$rlink$ 都是指向子结点指针，因此所有$ltag$和$rtag$ 的初始状态都为0。给出一棵二叉树，要 将它按对称序线索化，其做法就是按对称 序周游此二叉树，在周游的过程中用线索 代替空指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
void thread(ThrTree t){
    PSeqStack st = createEmptyStack(M);
    /*栈元素的类型是ThrTree，M一般取t的高度*/
    ThrTree p, pr;
    if(t==NULL)
        return ;
    p = t; pr = NULL;
    do{
        while(p!=NULL)
        {
            push_seq(st,p);
            p = p->link;
        }
        p=top_seq(st);
        pop_seq(st);
        if(pr!=NULL){
            if(pr->rlink==NULL){
                /*修改前驱节点的右指针*/
                pr->rlink=p;
                pr->rtag=1;
            }
            if(p->llink==NULL){
                /*修改该节点的左指针*/
                p->llink=pr;
                p->ltag=1;
            }
        }
        pr=p;p=p->rlink;
    }while(!isEmptyStack_seq(st)||p!=NULL);
}
按对称序周游对称序线索二叉树

要按对称序周游对称序线索二叉树，首先找到对称序列 中的第一个结点，然后依次找到结点的后继结点，直至其后继结点为空即可。
第一个结点很容易找，只要从根结点出发沿着左指针不断往下走，直至左指针为空，到达“最左下”的结点， 这就是对称序第一个结点。
找任意结点的对称序后继时，也非常容易做：一个结点的右指针字段如果是线索，则它就指向该结点在对称序 下的后继；如果不是线索，则它指向该结点右子树的根， 而该结点在对称序下的后继应是此右子树的最左下结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void nInOrder(ThrTree t){
    ThrTree p = t;
    if(t==NULL)
        return ;
    while(p->llink!=NULL && p->ltag==0)
        p=p->llink;
    while(p!=NULL){
        visit(*p);
        if(p->rlink!=NULL && p->rtag==0){
            /*右子树不是线索时*/
            p = p->rlink;
            while(p->llink!=NULL && p->ltag==0)
                p=p->llink;
            /*顺右子树的左子树一直向下*/
        }
        else 
            p=p->rlink;
    }
}